椭圆柱面，椭圆柱面图像

二次曲面是一种广泛存在的几何形态椭圆柱面，根据它们的标准方程，总共可以分为12种不同的类别以下是它们的详细描述圆柱面 Cyindrical surface x^2 + y^2 = a^2 椭圆柱面 Elliptic cylinder x^2a^2 + y^2b^2 = 1 双曲柱面 Hyperbolic cylinder x^2a^2 y^2b^2 =椭圆柱面；从方程上区分椭圆柱面和圆柱面的方法如下观察x2与y2的系数圆柱面在圆柱面的方程中，x2与y2的系数相等且均为正数这意味着，如果方程可以表示为Ax2+By2+Cz+D=0的形式，那么它表示的是一个圆柱面椭圆柱面在椭圆柱面的方程中，x2与y2的系数不相等或者其中之一为负数这意味着，如果。

椭圆柱面的母线

1、柱面有多种类型，主要包括以下几种一圆柱面 圆柱面是一个基本的柱面类型它以直线为基，围绕这条直线旋转所形成的面就是圆柱面在日常生活中，像铅笔的笔直的侧面树木的笔直部分等，都是圆柱面的实例这种柱面在数学和工程领域也有广泛应用二椭圆柱面 椭圆柱面是一种特殊的柱面类型，其。

2、这个式子放在二维坐标系中是椭圆曲线，如果再加一个Z轴，就变成了三维，也就是让这个椭圆曲线沿着Z轴做竖直上下运动，形成的图形就是一个椭圆柱面要形成锥面就需要有倾斜椭圆后，再围绕某一定直线旋转才能得到锥面注意一般得到锥面会有旋转因为不含有z，就有点类似于平面直角坐标系中x=3这条直线。

3、椭圆方程描述的是平面上的椭圆，可以用如下一般方程表示xaa + ybb = 1 其中a，b是椭圆的中心点坐标，a和b分别是横轴和纵轴的半轴长度这个方程表示的是平面上所有满足该方程的点构成的集合，也就是椭圆椭圆柱面方程描述的是三维空间中的椭圆柱面，可以用如下一般方程表示x。

4、柱面有多种类型，常见于数学和工程领域以下是几种常见的柱面1 圆柱面这是最基础的柱面形式在三维空间中，以一个直线为基础，作无数个平行且等距于这条直线的圆平面，这些圆平面所包围的面就是圆柱面在日常生活应用中，像柱子水桶壁等都是圆柱面的实例2 椭圆柱面椭圆柱面是由椭圆。

5、不是椭圆柱面是一种三维空间中的曲面，不能沿一个方向拉伸或压缩椭圆柱面在两个方向上都是无限的，即没有封闭的边界封闭曲面是指具有有限边界的曲面，球面或立方体表面由于椭圆柱面的无限性，不能被视为封闭曲面。

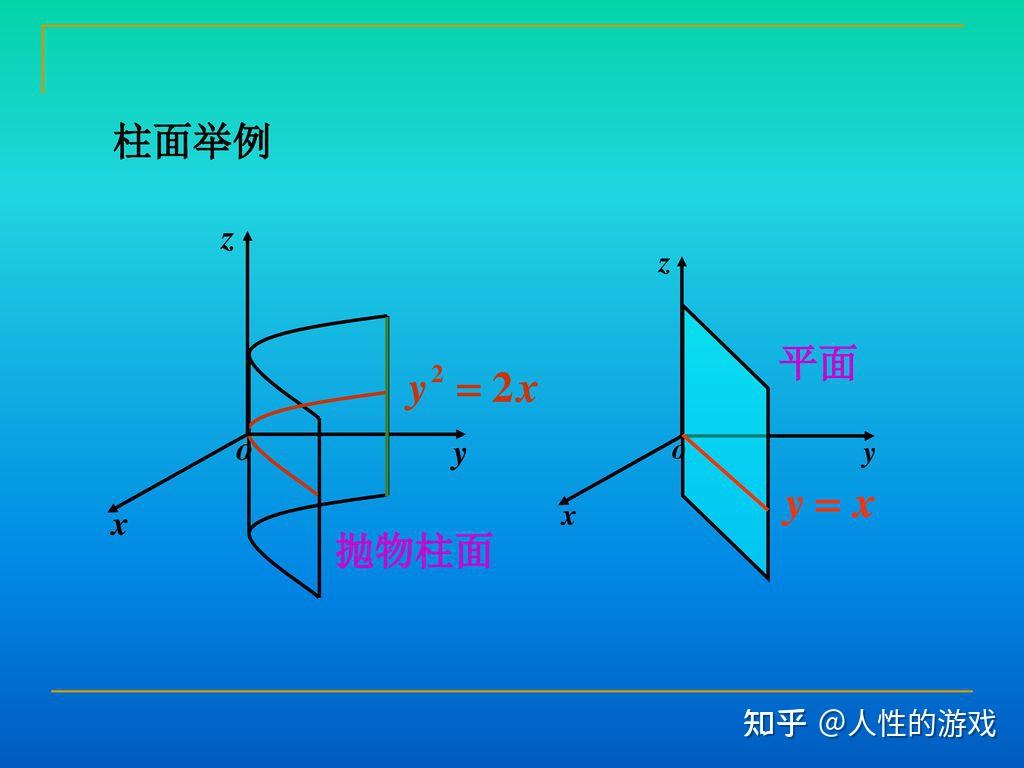
6、1抛物柱面 抛物柱面的方程是y#178=2px， 它的母线平行于Z轴，准线是XOY平面上以同样方程表示的抛物线2双曲柱面 双曲柱面的方程是它的母线平行于Z轴，准线是XOY平面上以同样方程表示的双曲线3椭圆柱面 椭圆柱面的方程是它的母线平行于Z轴，准线是XOY平面上以O为中心，a，b为半。

椭圆柱面怎么画

椭圆柱面的参数方程x = acosθ y = bsinθ 证明如下由 cos^2θ + sin^2θ = 1， 代入得x^2a^2 + y^b^2 = 1 lt==此为平行于z轴的椭圆柱面方程。

1柱面方程表达式对空间坐标系中Fx，y=0Gy，z=0Hx，z=0，这些都是柱面方程如x2+y2=1，就是圆柱面方程表达式2抛物柱面表达式y=x2双曲柱面表达式x2a2y2b2=1椭圆柱面表达式x2a2+y2b2=13直圆柱面如果直母线垂直于圆所在平面时，所得柱面称。

说明椭圆抛物面是一个形如椭圆的抛物面，其底面为椭圆，且关于z轴对称图片双曲抛物面 标准方程$fracx^2a^2fracy^2b^2=z 说明双曲抛物面是一个形如双曲线的抛物面，它有两个分支，且关于z轴对称图片椭圆柱面 标准方程$fracx^2a^2+frac。

使用Mathematica绘制椭圆柱面可以通过以下步骤完成首先，设置椭圆柱的尺寸参数，例如半轴a为3，半轴b为2在Mathematica中，可以使用参数a和b定义椭圆接着，使用ParametricPlot3D函数绘制椭圆柱面将上述定义的参数a和b代入函数中，其中第一对参数a Cost， b Sint表示在三维空间中椭圆的x和y。

理解柱面方程是区分椭圆柱面与圆柱面的关键考虑方程x^4 +y^4 +118x^2 +14y^2 +2x^2 y^2=0解析此方程，我们首先联立x2+y2+4z=1与x2=y2+z2通过消去z，我们得到x2+y2+4z=1，此式变换为4z=1x2y21接着，x2=y2+z2的等式两边扩大16倍，得到16z2 =16x216y22。

二次曲面是一系列由二次方程定义的几何形状，可以通过图形化的视角进行直观理解以下是对几种常见二次曲面的直观解释圆柱面可以想象成一张纸围绕其中心轴卷曲起来形成的三维结构它是平面通过拉伸而形成的一种简单的二次曲面椭圆柱面椭圆柱面是圆柱面的椭圆变体可以想象成椭圆形的纸片被拉长并。

1椭圆的方程是在平面直角坐标系里，表示X^2+y^2=r^2，是二维层面2椭圆柱面方程也是x^2+y^2=r^2，但是椭圆柱面他是在空间直角坐标系，是三维层面，还有个条件是以母线平行于z轴，沿着x^2+y^2=r^2的圆为准线绕完形成的曲面。

上一篇： 迅雷远程下载，迅雷远程下载设备

下一篇： 适合小学生读的课外书，小学生的课外书有哪些推荐