1、1 进入编辑模式首先贝塞尔曲线，选择贝塞尔曲线在3D视图中，按`Tab`键将进入编辑模式快捷键`Tab`您也可以在顶部菜单贝塞尔曲线的“视图”选项中找到“编辑模式”选项2 选择曲线在编辑模式中，选择要转换为实体的贝塞尔曲线您可以通过框选或使用快捷键`B`来选择曲线3 添加FCurve修改器在右侧的属性面板中，找到“修改器。
2、1创建贝塞尔曲线在正视图中，使用“样条画笔工具”或直接选择“贝塞尔样条”选项，在视图窗口中绘制一条基础曲线此时绘制的曲线包含节点，但节点上的控制手柄默认隐藏2显示控制手柄鼠标点击曲线上的某个节点，手柄会短暂显示若需持续显示手柄，需切换至正确的工具模式，避免因工具选择错误导致手柄消。
3、因为贝塞尔公式推导时用残差代替真误差，n个个残差中任何一个残差可以从另外n1个残差中推算出来，独立的残差项只有n1个，也就是自由度为n1可理解为被测量只有一个时，为估计被测量，只需测量一次，但为了提高测量的可信度而多测量了n1次，多测的次数可以酌情规定，所以称为自由度。
4、连续贝塞尔曲线Continuous Bézier curve是贝塞尔曲线的一种，它具有特殊的定义方式连续贝塞尔曲线由两个端点和一个控制手柄组成，其中每个控制手柄都可以自由调节，以改变曲线的形状与普通贝塞尔曲线相比，连续贝塞尔曲线具有以下特点连续性连续贝塞尔曲线在两个端点之间具有连续的切线，这意味着曲线在。
5、选中关键帧，右键“关键帧差值”，将“空间差值”换成“贝塞尔曲线”调节单个个手柄或者连续贝塞尔曲线两个一起调节，确定圆形关键帧，也属于平滑类关键帧，使动画曲线变得平滑可控，实现方法是按住ctrl键点击关键帧即可箭头形状关键帧，与上个关键帧类似，只是实现动画的一段平滑，包括入点平滑。
6、三阶贝塞尔曲线坐标公式为$B_3t=1 t^3P_0+3t1 t^2P_1+3t^21 tP_2+t^3P_3，tin0，1$n阶贝塞尔曲线可归纳总结出$n$阶贝塞尔曲线的坐标公式$Bt=sum_i = 0^nC_n^iP_i1 t^n it。
7、常用图形的贝塞尔曲线参数式主要包括一阶线性二阶二次三阶三次等形式，具体参数方程如下一阶贝塞尔曲线线性贝塞尔曲线给定两个控制点P_0x_0， y_0和P_1x_1， y_1，一阶贝塞尔曲线是一条连接这两个点的直线段参数方程为xt = 1tx_0 + tx_1，y。
8、一一阶贝塞尔曲线一阶贝塞尔曲线实际上是一条直线段，由两个顶点A和B组成利用线性插值原理，可以得到一阶贝塞尔曲线的轨迹公式Path = 1tA + tB 其中，t是一个参数，取值范围为0，1当t=0时，Path=A当t=1时，Path=B因此，随着t从0变化到1，Path将沿着线段AB从A移动到B。
9、贝塞尔曲线在路径规划中的平滑路径应用 贝塞尔曲线作为一种数学曲线，在二维图形设计中有着广泛的应用，特别是在矢量图的设计中然而，在路径规划中，贝塞尔曲线同样可以发挥重要作用，用于优化由各种搜索算法如RRT随机搜索算法得到的路径，使其更加平滑一贝塞尔曲线的基本概念 一阶贝塞尔曲线一阶。
10、贝塞尔曲线和B样条曲线是两种不同的曲线构造方法贝塞尔曲线定义贝塞尔曲线是一种在数学上用于绘制平滑曲线的技术，广泛应用于计算机图形学中它通过一组控制点来定义曲线的形状，这些控制点通过特定的算法如德卡斯特里奥算法生成曲线上的点特点平滑性贝塞尔曲线生成的曲线是平滑的，没有突变点。
11、在Blender中，贝塞尔曲线位于“添加”菜单的“曲线”选项列表中，具体查找步骤如下打开模型素材从电脑中选择一个模型素材，通过Blender的“文件”选项将其打开进入添加菜单在Blender界面上方找到并点击“添加”菜单选择贝塞尔曲线在展开的列表中打开“曲线”选项，即可在子列表中找到“贝塞尔曲线”。
12、在CorelDRAW中，若贝塞尔曲线断开成多段线条，可通过以下步骤连接并实现颜色填充核心操作步骤 基础绘制与节点定位 使用贝塞尔工具分别绘制两条独立曲线，确保两端节点位置对齐或预留重叠空间通过选择工具选中其中一条曲线，激活贝塞尔工具后点击该曲线末端的节点，此时光标会显示为可续接状态曲线续接与重叠。
13、在AE中将关键帧插值设为贝塞尔曲线，可让动态效果更自然，具体操作步骤如下第一步打开AE软件并创建动画启动After Effects，新建一个合成Composition，在时间轴中创建需要调整的动画效果例如，可通过“位置”“缩放”或“旋转”属性添加关键帧，形成基础动画序列第二步选中关键帧在时间轴面板中。
14、选中关键帧，右键“关键帧差值”，将“空间差值”换成“贝塞尔曲线”调节单个个手柄或者quot连续贝塞尔曲线quot两个一起调节，确定1首先我们打开ae软件2创建一个帧动画效果3然后选中关键帧4点击鼠标右键打开关键帧插值5然后在时间插值列表中选择贝塞尔曲线即可。
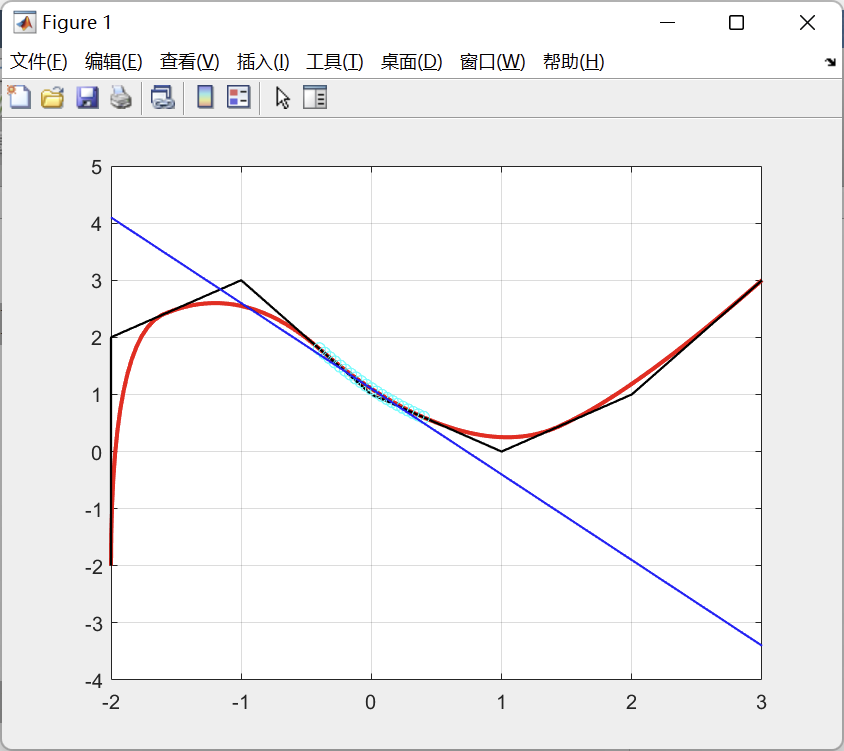
15、贝塞尔曲线Bézier Curves学习笔记1 前言贝塞尔曲线是一种在计算机图形学中广泛使用的参数曲线，它能够生成平滑且可控的曲线，非常适合用于动画路径字体轮廓图形界面设计等领域本文旨在记录对贝塞尔曲线的学习心得，特别是其背后的原理和实现方法2 原理Bézier Curvesde Casteljau Algorithm德。
16、贝塞尔曲线Bezier curve是一种广泛应用在计算机图形学和图像处理中的平滑曲线它通过一组控制点来定义曲线的形状，具有很高的灵活性和精度贝塞尔曲线的数学公式为Bt=1t^n*P_0+n*1t^n1*t*P_1++n！*t^n*P_n，其中t是参数，取值范围为0到1，Bt则表示曲线在。
相关标签 :
microsoft.netframework是什么，microsoft net framework在哪里
文件夹exe病毒专杀，电脑文件夹exe病毒专杀
ipad24.3.5越狱，ipad935为什么升不了级
网购火车票软件，购火车票的app
微信医疗（登记+咨询+回访）预约管理系统 联系电话：18300931024
在线QQ客服：616139763
官方微信：18300931024
官方邮箱： 616139763@qq.com
