综上所述,数学史上三次数学危机的三次危机分别是由无理数的诞生无穷小是否趋近于零的争议以及罗素悖论对康托尔集合论的挑战所引发的这些危机不仅推动三次数学危机了数学的发展,还促进了数学家们对数学基础的深入研究和重新审视。
第一次危机从有理数到实数,扩展了数的概念第二次危机从直观微积分到极限理论,确立了分析学的严谨性第三次危机从集合论到公理化方法,深化了对数学逻辑基础的理解这些危机证明,数学的发展本质上是“矛盾解决新矛盾新解决”的螺旋上升过程,而每一次突破都使数学更加接近真理。
数学发展史上的三次危机分别是无理数的发现导致的毕达哥拉斯悖论贝克莱悖论以及康托集合论中的悖论第一次数学危机公元前5世纪,古希腊数学家毕达哥拉斯学派在研究正五边形的对角线时,发现了无法用整数比表示的量,即无理数这一发现直接违反了毕达哥拉斯学派“万物皆数”的信条,因为按照他们的。
数学发展史上的三次危机分别是第一次数学危机时间公元前5世纪起因不可通约量的发现,即无理数的存在,这直接触犯了毕达哥拉斯学派的根本信条,毕达哥拉斯学派认为万物皆数,且数皆为有理数影响导致了当时认识上的危机,是数学史上的第一次重大危机第二次数学危机时间18世纪。
数学发展史上的三次危机分别是无理数的发现导致的毕达哥拉斯悖论贝克莱悖论以及康托集合论中的悖论第一次数学危机时间公元前5世纪起因不可通约量的发现,即无理数的存在这一发现直接触犯了毕达哥拉斯学派的“万物皆数”的根本信条,因为毕达哥拉斯学派认为所有的数都可以表示为两个整数。
数学史的三次危机分别是第一次数学危机起源公元前400年的毕达哥拉斯学派发现了无理数的存在影响这场危机冲击了毕达哥拉斯学派的哲学基础,并揭示了数学逻辑中的矛盾它催生了公理化体系的诞生,使数学与传统算术和现实世界有了清晰的界限第二次数学危机起源17世纪末,牛顿和莱布尼兹的。
数学发展史上的三次危机分别是1 第一次数学危机毕达哥拉斯悖论 时间公元前5世纪起因不可通约量的发现,直接触犯了毕达哥拉斯学派的根本信条,即“万物皆数”影响导致了当时数学界的认识危机,促使数学家们开始重新审视数的概念,推动了数学的发展2 第二次数学危机贝克莱悖论 时间。
数学发展史上的三次危机分别是1 第一次数学危机公元前5世纪,由不可通约量的发现导致的毕达哥拉斯悖论 背景毕达哥拉斯学派认为宇宙间一切事物都可归结为整数或整数之比,但无理数的发现打破了这一信条悖论毕达哥拉斯悖论指的是无理数的存在与毕氏学派的根本信条相冲突,即无法表示为两。
尽管三次数学危机带来的挑战未彻底解决,它们却促进了数学的深化和发展集合论的诞生,催生了抽象代数学和拓扑学的崭新领域,高维几何与数论的理论体系也日益完善二次大战后的数学,犹如繁花盛开,问题层出不穷,正是在与矛盾和危机的斗争中,数学取得了前所未有的繁荣每一次危机,都是数学前进的阶梯。
三第三次数学危机集合论中的悖论 时间1897年背景集合论是现代数学的基础之一,但在19世纪末,数学家福尔蒂提出了一个关于理发师的悖论,这个悖论满足了集合论的原理,但却得出了自相矛盾的结论危机起因理发师悖论揭示了集合论中的漏洞,如果这个悖论不解决,集合论就是有漏洞的,进而影响。
即一个集合如果包含了它自身作为元素,那么这个集合就会陷入自相矛盾的境地这一悖论引发了数学界的混乱与反思,推动了数学家们对数学基础的重新审视和重构,从而催生了第三次数学危机这三次危机不仅揭示了数学理论的局限,也推动了数学理论的革新和深入探索,对数学的发展产生了深远的影响。
2公理化集合系统,成功排除了集合论中出现的悖论,从而比较圆满地解决了第三次数学危机但在另一方面,罗素悖论对数学而言有着更为深刻的影响它使得数学基础问题第一次以最迫切的需要的姿态摆到数学家面前,导致了数学家对数学基础的研究而这方面的进一步发展又极其深刻地影响了整个数学如围绕着。

导致了数学史上的第二次危机第三次危机罗素悖论的挑战 罗素悖论通过一系列反直觉的问题挑战了集合论的基础,揭示了集合论中的悖论和矛盾这类问题引发了人们对数学基础的重新审视,构成了数学史上的第三次危机虽然这些危机曾给数学的发展带来困扰,但它们也推动了数学的不断进步和完善。
简述三次数学危机及其意义如下危机一,希巴斯Hippasus,米太旁登地方人,公元前470年左右发现了一个腰为1的等腰直角三角形的斜边即2的2次方根永远无法用最简整数比不可公度比来表示,从而发现了第一个无理数,推翻了毕达哥拉斯的著名理论相传当时毕达哥拉斯派的人正在海上,但就因为。
牛顿和莱布尼茨的微积分理论缺乏严格的逻辑基础,特别是无穷小量的概念模糊不清,导致了第二次数学危机直到19世纪,柯西魏尔斯特拉斯等人建立了极限理论,才为微积分提供了坚实的基础第三次数学危机起源于1897年,与集合论中的悖论有关康托的一般集合理论在数学中占据重要地位,但它却引发了一。
数学的三次危机是无理数的发现集合论的悖论费马大定理的证明1无理数的发现 在公元前5世纪,希腊数学家毕达哥拉斯发现了一个无法用整数表示的数,即无理数这个发现挑战了当时数学的基本原则,即所有的数都可以表示为整数或分数这个发现对数学产生了深远的影响,导致数学家们重新审视数学的。
 windowsxp系统修复,winxp系统修复命令具体操作
windowsxp系统修复,winxp系统修复命令具体操作 空间音乐播放器代码,空间音乐播放器代码是什么
空间音乐播放器代码,空间音乐播放器代码是什么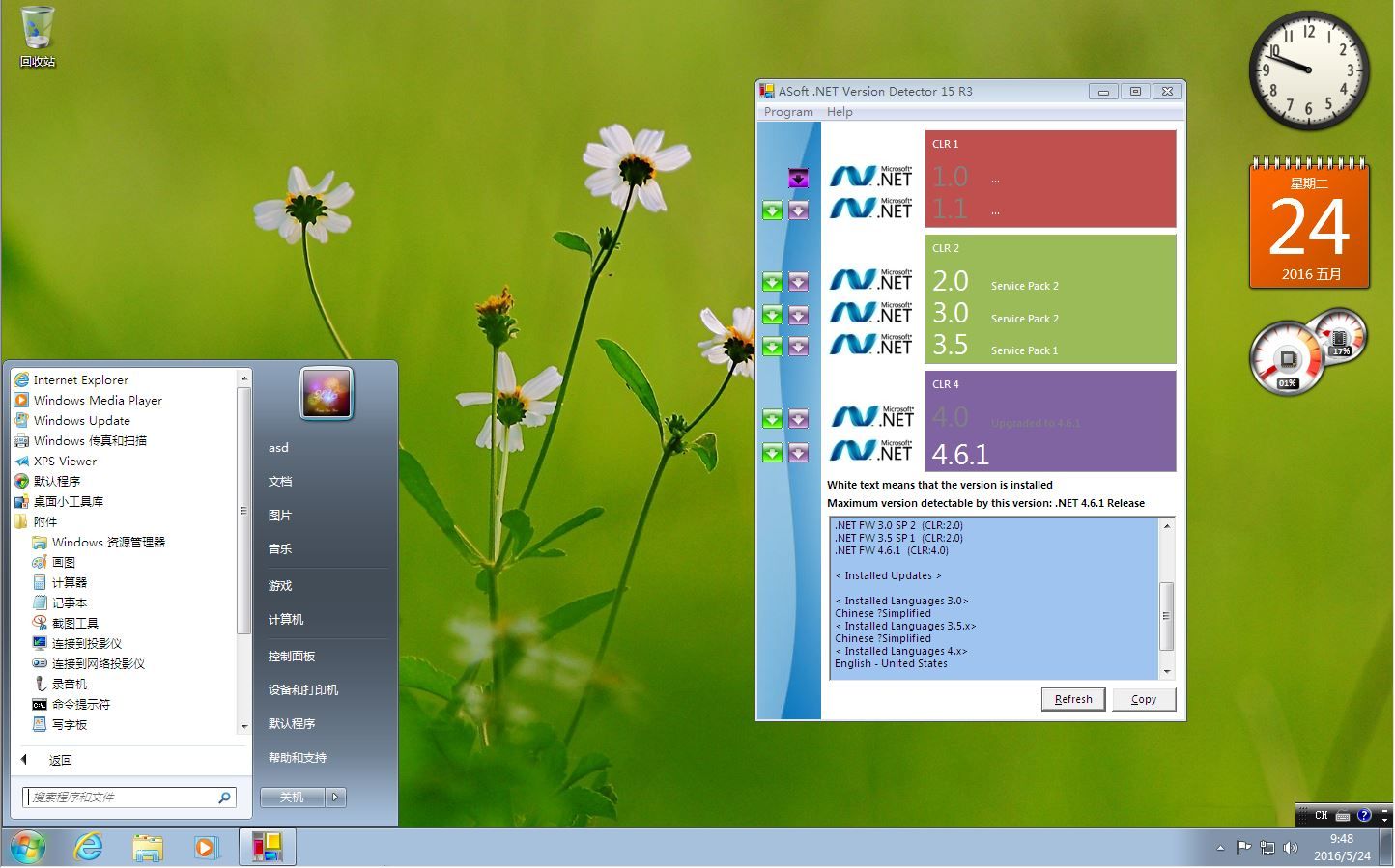 专注于win7,专注于win7唯一官网
专注于win7,专注于win7唯一官网 microsoft.netframework是什么,microsoft net framework在哪里
microsoft.netframework是什么,microsoft net framework在哪里 文件夹exe病毒专杀,电脑文件夹exe病毒专杀
文件夹exe病毒专杀,电脑文件夹exe病毒专杀 ipad24.3.5越狱,ipad935为什么升不了级
ipad24.3.5越狱,ipad935为什么升不了级联系电话:18300931024
在线QQ客服:616139763
官方微信:18300931024
官方邮箱: 616139763@qq.com
