一作差构造法 直接作差构造通过直接减去函数的某部分来构造新的函数导数构造函数技巧,利用导数求解变形作差构造改变原函数表达式,通过变形后作差构造新函数,再利用导数求解二分离参数构造法 将变量分离,构造函数,利用导数解决参数问题三局部构造法 1 化和局部构造将和式分解,局部构造函数求解2。
直接构造法方法根据题目给出的f与frsquo的关系,直接构造出F示例若frsquo f,可构造F = e^x * f乘除构造法方法通过乘以或除以某个函数,使得新函数的导数易于分析示例若frsquo + f 0,可构造F = e^x * f加减构造法方法对f进行加减运算,结合其导数。
首先,根据已知表达式的形式结合所求表达式,构造一个新的函数Fx这个步骤的关键在于,通过巧妙地构造Fx,使得它与原问题中的条件紧密相关其次,分析并讨论新函数Fx的单调性奇偶性等形式,以及特殊点赋值通过这些分析,我们可以更好地理解Fx的性质,为后续的解题提供依据最后。
模型3,若出现fx与f#39x系数分别是常数和x时,考虑构造xquot与fx的积或者商模型4,若出现fx与f#39x且系数为sinx与COSx时,考虑构造sinx与fx的积或者商,或者cosx与fx的积或者商构造辅助函数是求解导数问题的常用策略,而构造函数的方法技巧较为众多,需要结合具体。
方法6 构造二阶导数函数来证明函数的单调性 这种方法在高考导数综合问题中,经常要用到的一个技巧 方法7 对数法构造函数适用于幂函数不等式对数法构造函数的适用条件就是对于指数型不等式或幂函数不等式类型的证明问题方法8 构造形似函数 通过对不等式进行等价转化,变成形似相近的两个式子,可以。
总之,构造函数放缩是一种在高中导数题解题中非常有用的技巧,通过恰当选择放缩函数,我们可以简化问题,降低证明难度在实际应用中,合理利用泰勒公式和帕德近似等方法,能够有效提高解题效率和准确度通过对各种函数的深入理解,结合图像观察和计算辅助,我们可以更好地掌握构造函数放缩的精髓,从而在高中。
一利用fx进行抽象函数构造1利用fx与x构造常用构造形式有xfx,数导数计算的推广及应用,我们对uv,fxu这类形式是对uv,型函xvu体现的是“”法,型导函数中体现的是“”法,由此,我们可以猜测,当v导函数形式出现的是“”法形式时,优先考虑构造uv型,当导函数形式出现u的是。
一移项法构造函数 方法说明通过移项,将不等式的一侧转化为0,然后将另一侧设为新的函数,利用导数研究该函数的单调性或最值,从而证明不等式示例二作差法构造函数 方法说明直接对不等式两边作差,构造出新的函数,然后利用导数研究该函数的单调性,从而证明不等式示例三换元法构造。
通过二阶导数的符号变化,可以判断曲线的凹凸性二阶导数等于零的点可能是拐点三经典解题技巧 构造函数法在解决不等式问题时,可以通过构造函数并利用导数的性质来判断不等式的真假参数分离法在处理含参函数问题时,可以通过参数分离将问题转化为求函数的最值问题放缩法在证明不等式时,可以。
极值问题 题型描述求函数的极大值极小值或最值答题技巧先求导数,令导数等于0找到可能的极值点,再结合单调性判断极值点的性质极大值或极小值,最后比较各极值点和端点处的函数值确定最值不等式证明 题型描述利用导数证明不等式答题技巧构造函数,利用导数判断函数的单调性,结合单调性证明不等式有时需要利。
根据单调性判断极值点极大值或极小值最值问题 题型描述求函数在给定区间上的最大值或最小值解题技巧首先求出函数的一阶导数令一阶导数等于0,结合区间端点,确定可能的极值点比较各极值点和区间端点的函数值,确定最值不等式证明 题型描述利用导数证明不等式解题技巧构造函数。
根据题目给出的条件或不等式的特征,直接或经过变形后构造函数进行证明主元构造函数法在处理多元不等式或多变量组成的复杂不等式时,选定其中一个变量作为主元,围绕该主元构造函数构造二阶导数函数来证明函数的单调性在研究函数的单调性时,通过构造二阶导数函数,利用其符号变化来判断原函数的单调。
如同构的替代品极值点偏移选择题中构造函数问题,建议读者参阅其他文章以获取更全面的导数构造函数技巧了解此外,文章中还涉及到函数性质的应用,如周期函数的导数性质函数关于点的对称性等以上内容为解题策略提供了一定的思路和方法,但请注意,实际应用时需根据具体问题灵活调整,并结合其他数学知识和技巧。
解决实际应用问题 如优化问题如面积最大成本最低等,常通过建立函数模型,利用导数求解三导数题型的解题技巧 构造函数法通过构造函数,利用导数的性质求解问题数形结合法结合函数图像,直观判断函数的单调性极值等性质分类讨论法对于含参数的问题,常需对参数进行分类讨论,分别求解。
导数构造函数是一种常用的数学工具,它可以帮助我们更好地理解和分析函数的性质在实际应用中,有许多常用的导数构造函数模型,以下是其中的一些1幂函数模型幂函数是最基本的导数构造函数模型之一,它的形式为fx=ax^n,其中a和n都是常数通过求导,我们可以得到f#39x=nax^n12指数。
高考导数不等式证明方法凹凸反转 凹凸反转是一种在导数不等式证明中常用的技巧,尤其适用于那些极值点难以直接求解的情况以下是对凹凸反转方法的详细解释和步骤说明一凹凸函数的定义 凹函数如果函数$fx$在区间$I$上连续,且对$I$上任意两点$x_1, x_2$,恒有$fracfx_1+fx_。
题型描述利用导数证明不等式解题思路构造函数,利用导数判断函数的单调性,从而证明不等式常见的方法有拉格朗日中值定理泰勒公式展开单调性分析等五零点问题 题型描述判断函数的零点个数,或求解函数的零点解题思路利用导数判断函数的单调性,结合零点存在定理如介值定理判断零点的。
注意还需检验驻点两侧的函数值,确保极值的准确性切线问题利用导数求解给定点的切线斜率,进而求出切线方程公式切线斜率$k = f#39x_0$,切线方程为$y fx_0 = kx x_0$不等式证明构造函数,利用导数判断函数的单调性,从而证明不等式技巧常通过放缩法构造函数法。

相关标签 :
上一篇: 产品生命周期,产品生命周期四个阶段
下一篇: 关于红帽认证考试费用2019的信息
 windowsxp系统修复,winxp系统修复命令具体操作
windowsxp系统修复,winxp系统修复命令具体操作 空间音乐播放器代码,空间音乐播放器代码是什么
空间音乐播放器代码,空间音乐播放器代码是什么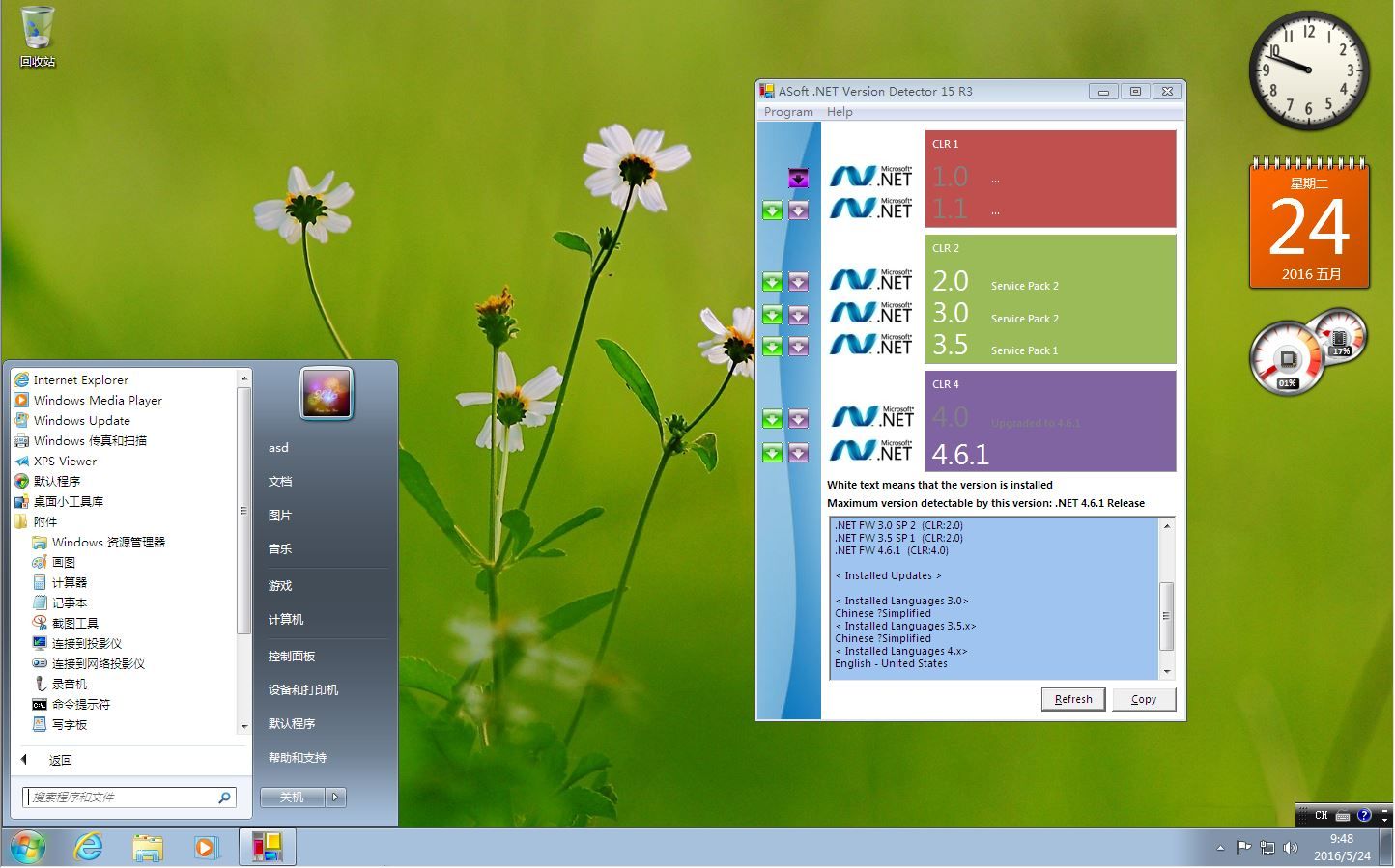 专注于win7,专注于win7唯一官网
专注于win7,专注于win7唯一官网 microsoft.netframework是什么,microsoft net framework在哪里
microsoft.netframework是什么,microsoft net framework在哪里 文件夹exe病毒专杀,电脑文件夹exe病毒专杀
文件夹exe病毒专杀,电脑文件夹exe病毒专杀 ipad24.3.5越狱,ipad935为什么升不了级
ipad24.3.5越狱,ipad935为什么升不了级联系电话:18300931024
在线QQ客服:616139763
官方微信:18300931024
官方邮箱: 616139763@qq.com