曲率中心坐标，某点曲率中心坐标

1、曲率中心坐标公式推导如下首先需要假设曲率k=y#39#391+y#39^2^32曲率中心坐标，在前面的式子中曲率中心坐标，可以假设其中y#39，yquot分别为函数y对x的一阶和二阶导数1需要进行假设曲线rt =xt，yt，曲率k=x#39yquot xquoty#39x#39^2 + y#39^2^32，然后进行求导得到第二步2设曲线rt为三维向量函数。

2、曲率中心坐标，曲线上任一点对应的曲率中心坐标公式的推导过程如下曲线上点M处的曲率的倒数，称作曲线在这点处的曲率半径，记作p ，则 在点M处曲线的法线的某一侧上取一点D，使DM=p，并以D为圆心，以p为半径作圆把这个圆称作曲线在点M处的曲率圆，把圆心D称做曲线在M处的曲率中心在某。

3、曲率中心坐标公式推导如下首先需要假设曲率k=y#39#391+y#39^2^32，在前面的式子中，可以假设其中y#39，yquot分别为函数y对x的一阶和二阶导数1需要进行假设曲线rt =xt，yt，曲率k=x#39yquot xquoty#39x#39^2 + y#39^2^32，然后进行求导得到第二步2。

4、曲率中心坐标是描述曲线在某一点弯曲程度和方向的几何量，它表示该点附近曲线段的最佳拟合圆的圆心坐标关于曲率中心坐标，可以归纳以下几点定义对于平面曲线上的某一点，曲率中心坐标即为该点附近曲线段最佳拟合圆的圆心坐标这个拟合圆被称为“密切圆”或“曲率圆”变化性曲率中心坐标并非一个。

5、曲率中心坐标的求解方法主要依赖于曲线的曲率公式以及该点的切线斜率以下是求解曲率中心坐标的步骤一理解曲率公式 曲率公式为 k = y#39 1 + y#39^2^32，其中 k 表示曲率，y#39 表示曲线在该点的切线斜率这个公式描述曲率中心坐标了曲线在某一点的弯曲程度，是求解曲率中心的关键二计算。

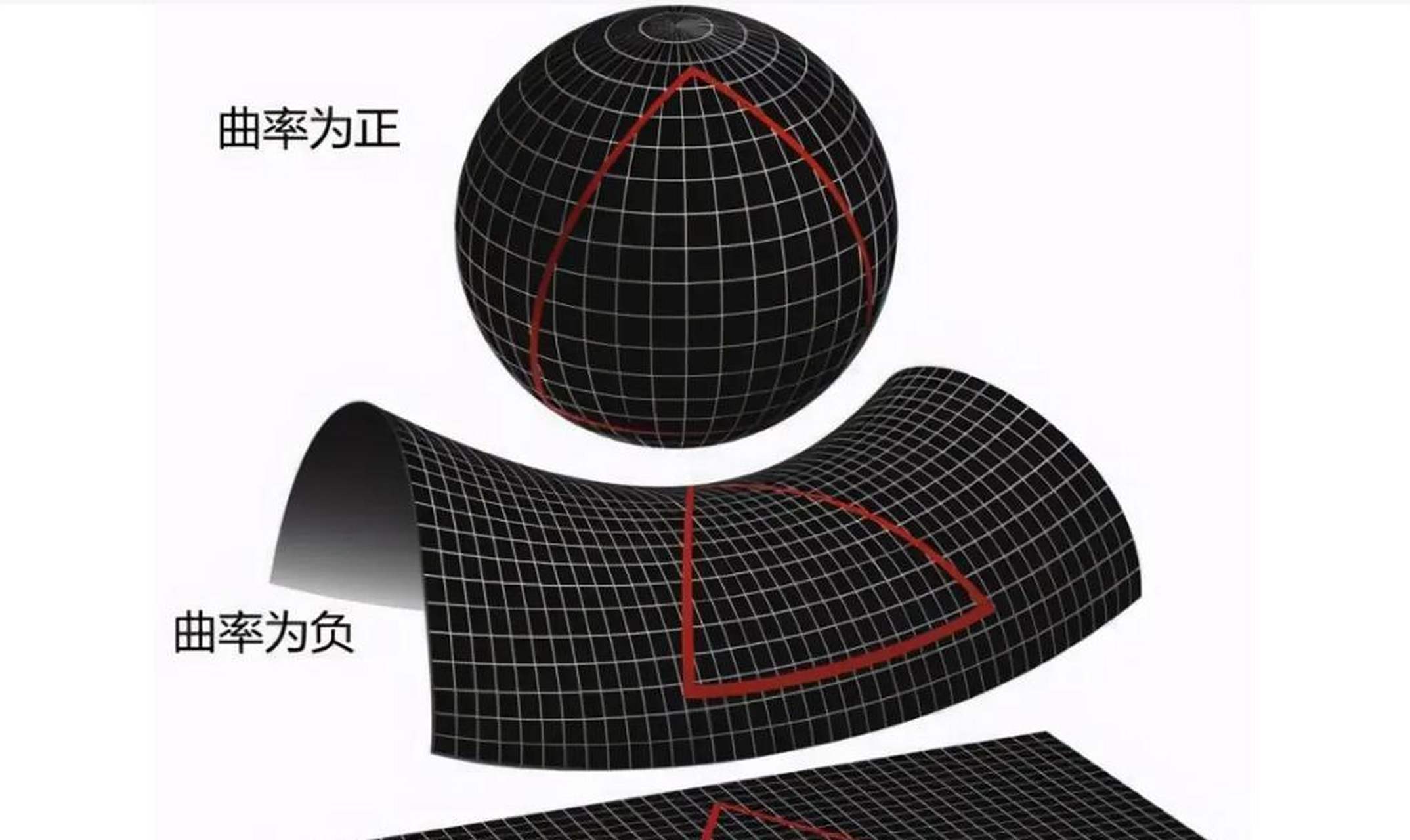
6、曲率中心坐标的公式及相关内容如下二维曲线曲率公式对于二维曲线 $y = f$，其曲率 $k$ 的公式为$k = fracyrdquo^2^frac32$其中，$yrsquo$ 和 $yrdquo$ 分别为函数 $y$ 对 $x$ 的一阶和二阶导数参数方程形式的二维曲线曲率公式设曲线 $r = 。

7、曲率中心坐标是k=y#391+y#39^2^32曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率，通过微分来定义，表明曲线偏离直线的程度数学上表明曲线在某一点的弯曲程度的数值曲率是几何体不平坦程度的一种衡量平坦对不同的几何体有不同的意义欧几里得空间中的曲线和曲面的。

8、曲率中心坐标是描述曲线上某点处曲率特性的重要几何量在微分几何中，对于一条平滑曲线，其上任一点的曲率中心定义为通过该点并与曲线在该点具有相同切线方向和曲率圆的圆心曲率中心坐标的计算依赖于曲线的参数方程或显式方程，以及该点的具体位置具体来说，若曲线在某点处的曲率半径为R，且该点。

9、曲率中心坐标，在几何学中，特指曲线上某点处曲率圆的圆心坐标这一概念对于理解曲线的局部形状特征至关重要对于给定的曲线，其上任一点的曲率中心坐标并非固定不变，而是随着所取点的不同而变化计算曲率中心坐标通常涉及曲线的导数尤其是二阶导数，这些导数反映曲率中心坐标了曲线在该点处的弯曲程度和方向。

10、曲率中心坐标的求解方法涉及多个步骤，并且通常需要根据具体的曲线方程来推导以下是一个一般性的求解思路确定曲线方程首先，需要明确曲线的方程，通常表示为 $y = f$计算一阶导数对曲线方程 $y = f$ 求一阶导数 $y’$，表示曲线在该点的切线斜率计算曲率使用曲率公式 $k = fracy。

11、曲率中心坐标是描述曲线在某一点弯曲程度和方向的几何量，它通常用于圆或圆弧的近似描述，在微分几何工程学物理学和计算机图形学等领域有广泛应用不过，曲率中心坐标并非一个固定值，而是随着曲线上点的位置变化而变化在详细解释之前，需要曲率中心坐标了解曲率中心的基本概念对于平面曲线上的某一点，其曲率中心可以看作是这一点附近曲线段的最佳。

12、圆曲率中心坐标的求解方法主要依赖于确定曲率半径和法线方向以下是具体的求解步骤确定曲率半径在曲线上的某一点M处，曲率的倒数被定义为该点的曲率半径，通常用p来表示曲率半径p可以通过曲线的方程和微分几何的知识来求解确定法线方向在点M处，需要确定曲线的法线方向法线方向可以通过曲线的。

13、曲率圆的圆心坐标没有具体公式，只能通过半径，求出来求曲线，该点求斜率求出法线方程，由该点坐标和半径就可以求出圆心坐标但是一般函数Y=FX的曲率中心D横坐标是m纵坐标是n则M=XY的导数，产生一个y的导数的平方加1再除以Y的二导数 N=Y+1括号Y的导数的平方，再加1÷Y的两次导数。

14、求出法线方程利用切线斜率和点斜式方程，可以求出曲线在该点的法线方程利用曲率半径和法线方程求解圆心坐标圆心位于法线上，且与曲线上的该点距离等于曲率半径因此，可以通过设立方程来求解圆心坐标对于一般函数$Y=FX$，如果其曲率中心D的横坐标是m，纵坐标是n，则可以通过以下方式求解m和n。

15、五曲率中心的坐标公式 对于显式方程$y = fx$，若二阶导数$f#39#39x$在点$x$不为0，则曲线在点$Mx， y$处的曲率中心$Da， b$的坐标可以通过以下公式计算其中，$f#39x$和$f#39#39x$分别为函数$fx$在点$x$处的一阶和二阶导数六曲率圆的应用 辅助理解曲线弯曲程度。

上一篇： vs2013连接sql数据库，vs2013怎么连接sql数据库

下一篇： 电脑排版教程视频，电脑排版怎么操作视频教程