参数方程是在直角坐标系中选中一个参数 并用该参数表示曲线上的任意点的横坐标和纵坐标构成方程组极坐标是另一种的坐标系极坐标与参数方程,它的坐标系只有极角和极径,极坐标方程就是用极径和极角表示曲线上点的方程极坐标与参数方程;要将平面直角坐标系中的参数方程化为极坐标方程,一般来说有两种常用方法 先将参数方程化为普通方程,再根据极直互化公式化为极坐标方程,具体过程如下根据方程所表示的图形直接写出其极坐标方程由于参数方程表示了圆心坐标为1,0,半径为1的圆,在极坐标系中,其圆心坐标仍为1,0,半径为1;极坐标参数方程 1首先极坐标是个坐标,不是方程不能说极坐标是参数方程曲线的直角坐标方程极坐标方程及参数方程只是曲线的3种表达方式,可以相互转化2参数方程转化为曲线方程就是找到xy之间的关系,消去参数3参数方程的参数t和极坐标里的θ没有什么必然关系θ是在极坐标系里曲线上一点。
曲线的参数方程和普通方程是曲线方程的不同形式一般的,可以通过消去参数从而参数方程得到普通方程如果知道变数x,y中的一个于参数t的关系,例如x=ft,把它代入普通方程,求出另一个变数于参数的关系y=ft,那么x=ft,y=gt就是曲线的参数方程极坐标与直角坐标的互化把直角坐标系;星形线的参数方程为begincasesx = rcos^3 t y = rsin^3 tendcases其中,r为小圆的半径,t为参数若消去t,可得星形线的直角坐标系方程为x^frac23 + y^frac23 = r^frac23总结极坐标系和参数方程是描述平面上点位置和曲线形状的两种重要方法极坐标系通过极径和极角来确定点的位置,而参数方程则通过引入新变量来表示曲线的;极坐标方程转化为参数方程,一般需要以下方式转化过程 1首先,需要确定极坐标系中的两个基本元素极径ρ和极角θ2然后,将极径和极角的值代入极坐标方程,得到参数方程的参数t3最后,利用参数t,结合极坐标系中的极径和极角,得到参数方程的x和y值 具体来说,对于极坐标方程ρ= 2cos;极坐标与参数方程知识点极坐标 定义在平面内取一个定点O,叫极点,引一条射线Ox,叫做极轴,再选定一个长度单位,一个角度单位,这样平面内任意一点P的位置就可以用线段OP的长度ρ和OP与Ox所夹的角θ来确定,有序数对就叫做点P的极坐标,其中ρ叫做点P的极径,θ叫做点P的极角 极坐标与直角;极坐标与参数方程公式如下极坐标公式 基本转换公式 $x = rhocostheta$ $y = rhosintheta$ $tantheta = fracyx$ 极坐标方程用极坐标系描述的曲线方程称作极坐标方程,通常表示为 $rho$ 为自变量 $theta$ 的函数,即 $rho = f$ 对称性如果 $rho =;极坐标和参数方程的主要区别如下描述方式极坐标侧重于极径和极角的定义极径表示点与原点之间的距离,极角则指示该点与极轴的连线与极轴正方向之间的角度在极坐标系下,点的坐标以 的形式呈现参数方程强调参数变化对坐标的影响x 和 y 被表示为 x=f 和 y=g 的函数,t 作为参数;极坐标与参数方程作为描述平面上点的两种方式,它们在表示点的位置上存在差异极坐标通过极径和极角来定位,而参数方程则通过参数变量完成两者虽形式不同,但功能相通,均可描绘出如圆椭圆双曲线等平面图形极坐标方程能通过参数方程找到曲线上各点坐标,反之亦然选择合适的方程形式取决于所需。
极坐标与参数方程公式是x=gt,y=ht,x=gt,y=ht,x=gt,y=ht 坐标系与参数方程是极坐标与参数方程我们必考的选修内容通过对近几年全国卷及各省真题的分析,我们可以发现,这部分的考查主要集中在坐标系的相互转化,参数方程极坐标方程与曲线的综合应用,包括点与直线的位置关系,直线;高考数学冲刺营选修44坐标系与参数方程核心要点如下一核心知识点梳理坐标系变换 极坐标与直角坐标互化公式 x = rho costheta , y = rho sintheta rho^2 = x^2 + y^2 , tantheta = fracyx 参数方程与普通方程互化通过消参法将参数方程转化为普通方程,需注意。

极坐标和参数方程的主要区别如下定义与表示方法参数方程是通过引入一个或多个参数来描述一个曲线或曲面的方程在二维平面上,一个曲线的参数方程通常表示为x=f,y=g的形式,其中t是参数极坐标是一种二维坐标系统,用极径ρ和极角θ来表示平面上的点其中,ρ表示点到原点的距离,θ表示;极坐标与参数方程公式如下极坐标方程的基本公式x = ρcosθy = ρsinθtanθ = yx其中,ρ表示点到原点的距离,θ表示点与正x轴之间的夹角极坐标方程的对称性质如果ρθ = g其中,t为参数圆的参数方程x = a + rcosθy = b + rsinθ其中,为圆心坐标,r为圆半径,θ为;由极坐标方程求参数方程,核心方法是将极坐标变量$r, θ$转换为笛卡尔坐标$x, y$,通过代入极坐标方程得到参数方程具体步骤如下1 极坐标与直角坐标的转换关系极坐标$r, θ$与直角坐标$x, y$的转换公式为$$x = r cosθ, quad y = r sinθ$$其中,$r$表示点到原点的。

相关标签 :
上一篇: 姓名电码查询,美国签证姓名电码查询
 windowsxp系统修复,winxp系统修复命令具体操作
windowsxp系统修复,winxp系统修复命令具体操作 空间音乐播放器代码,空间音乐播放器代码是什么
空间音乐播放器代码,空间音乐播放器代码是什么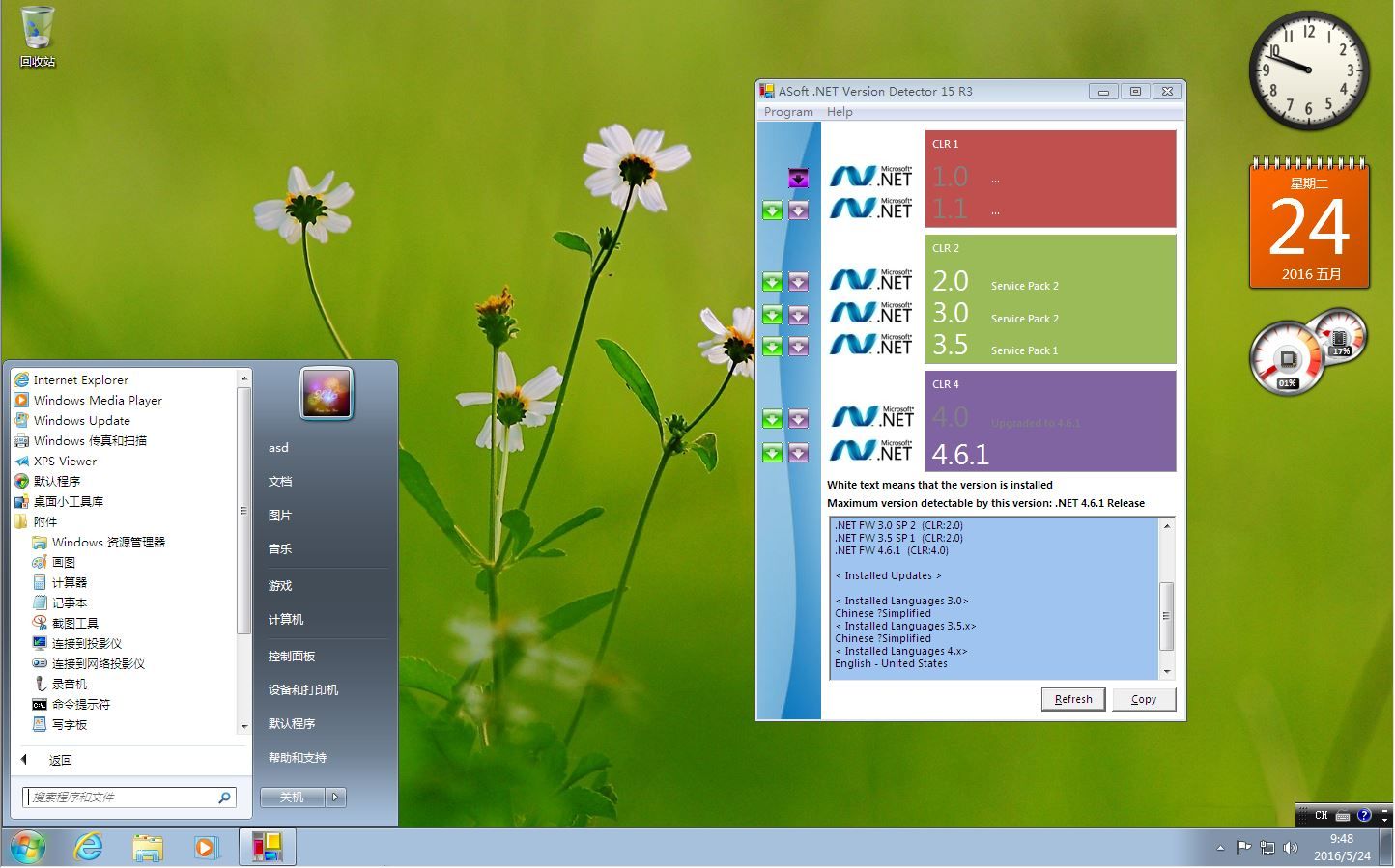 专注于win7,专注于win7唯一官网
专注于win7,专注于win7唯一官网 microsoft.netframework是什么,microsoft net framework在哪里
microsoft.netframework是什么,microsoft net framework在哪里 文件夹exe病毒专杀,电脑文件夹exe病毒专杀
文件夹exe病毒专杀,电脑文件夹exe病毒专杀 ipad24.3.5越狱,ipad935为什么升不了级
ipad24.3.5越狱,ipad935为什么升不了级联系电话:18300931024
在线QQ客服:616139763
官方微信:18300931024
官方邮箱: 616139763@qq.com