csc函数，csc函数与sin函数的关系

sec和csc函数csc函数的诱导公式及图像特点如下诱导公式1 周期性 sec = secα csc = cscα 其中k为整数，这表明当角度增加2kπ时，sec和csccsc函数的值保持不变补角关系sec = secαcsc = cscα这表明sec和csc在π的补角处取相反值负角度关系sec = secαcsc = cscα这表明sec函数在；sinα cosα tanα等三角函数的定义在一个直角三角形中，两直角边长分别是 a，b，斜边长为 c角 α 的对边为 asinα=ac cosα=bc tanα=ab cotα=ba secα=cb cscα=ca 区别。

定义余割函数csc x定义为正弦函数sin x的倒数，即csc x = 1sin x在直角三角形中，余割可以理解为斜边与对边的比值但通常不这样直接理解，因为余割更常通过与其他三角函数的关系来定义和使用几何意义虽然余割在直角三角形中不直接表示为斜边与对边的比值，但可以通过与其他三角函数的关系；csc的原函数是正弦函数sin详细解释如下1 定义与概念理解csc是余割函数的缩写，它是对正弦函数进行倒数运算得到的函数因此，当csc函数我们考虑其原函数时，自然联想到正弦函数sin原函数指的是反函数通过对数运算得到的新函数，所以csc的反函数即为正弦函数sin2 数学推导从数学的角度来看，余割函数。

三角函数中的 sec 和 csc 是 secant正割和 cosecant余割的简写，它们是三角函数中的两种常用函数 1 正割sec正割函数是指三角函数中的一种，表示为 secx正割是余弦函数cos的倒数，即 secx = 1cosx正割函数在直角三角形中定义为斜边与邻边的比值 2 余割csc余割函数是指三；csc是余割函数，是三角函数的一种以下是关于csc函数的详细解释定义余割函数，记作csc，是基于圆的半径和角度关系得出的具体来说，余割函数是圆的直径相对于该圆上某个点的正弦值的倒数对于给定的角度θ，其对应的余割值等于该角度的正弦值的倒数性质余割函数具有周期性，其周期是π余割。

三角函数csc是余割函数，是在直角三角形某个锐角的斜边与对边的比，用 csc角表示 常见的三角函数包括正弦函数sin余弦函数cos和正切函数tan 或者tg在航海学测绘学工程学等其他学科中，还会用到如余切函数正割函数余割函数正矢函数半正矢函数等其他的三角函数函数中；三角函数csc是余割函数，是在直角三角形某个锐角的斜边与对边的比，用 csc角表示 一个角的顶点和该角终边上另一个任意点之间的距离除以后一个点的非零纵坐标所得之商，这个角的顶点与平面直角坐标系的原点重合，而其始边则与正X轴重合，记作cscx余割与正弦的比值表达式互为倒数余割的函数图像为奇函数，且为周期函数。

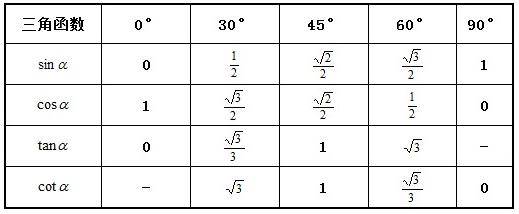
为csc函数了求出sec和csc在给定角度的值，csc函数我们需要先找到这些角度的余弦和正弦值，然后分别取它们的倒数以下是0°，30°，45°，60°，90°，120°，135°，150°，180°这些角度对应的sec和csc值1 0°sec0° = 1cos0° = 11 = 1 csc0° = 1sin0° = 10 不存在。

csc函数积分

在单位圆上，余割函数表现为与正弦函数相似但方向相反的变化趋势在角度从0增加到π的过程中，余割函数值从无穷大逐渐减小到接近零的值，然后随着角度的进一步增加，其值再次逐渐增大到接近无穷大的值这种周期性变化是余割函数的基本特征此外，余割函数具有偶函数的性质，即csc=cscθ这表明余割函数。

csc定义角的对边与从顶点到终边任意点距离的比值，在直角坐标系中，cscx等于1sinx关系在直角三角形中，它对应于斜边与锐角的对边比值注意csc函数与正弦函数互为倒数这些三角函数在高中数学课程中通常会被学习，它们在理论计算图形描绘以及周期性质的理解中起到关键作用。

csccosecant是余弦三角函数，读音美kosiknt英ksiknt三角函数是数学中属于初等函数中的超越函数的函数它们的本质是任何角的集合与一个比值的集合的变量之间的映射通常的三角函数是在平面直角坐标系中定义的其定义域为整个实数域另一种定义是在直角三角形中，但并不完全现代数学把。

sin 读作 赛因sinecos 读作 苦赛因cosinetan 读作 探今踏tangentcot 读作 苦探今他cotangentsec 读作 sec 思A肯特secant，发音为 secant，音标为#39sik#601ntcsc 读作 抠思A肯特cosecant，发音为 cosecant，音标为，k#601u#39sik#601nt这些三角函数在几何。

csc函数的图像和性质

1、导数是数学中的一个重要概念，csc是其中一个常用的函数，它有什么意义呢csc是余切函数的倒数，用来计算角度的正切值的倒数在三角函数中，csc代表正弦函数的倒数，其全称是cosecantcsc的存在使得我们在解决一些复杂的三角函数问题时能够更加简单明了地进行计算在求导数中，csc的使用频率很高，它在。

2、csc是余割三角函数以下是关于csc函数的详细解释一定义 余割函数csc角定义为在直角三角形中，某个锐角的斜边长度与该锐角的对边长度之比在直角坐标系中，若一个角的顶点与坐标原点重合，其始边与正X轴重合，则该角的余割值cscx等于原点到该角终边上任意一点P的距离OP除以点P的纵坐标y。

3、在数学领域，特别是三角函数中，csc代表的是余割函数，它是正弦函数sin的倒数这意味着，对于任何非零的角度theta其正弦值不为0，csctheta等于1除以sintheta余割函数在数学公式和实际应用中起着重要的作用，尤其是在处理与角度波动周期现象等相关的问题时当我们谈论三角函数时，我。

4、详细解释如下在数学中，csc函数实际上是正弦函数sin的倒数正弦函数sin是基本的三角函数之一，其定义域为全体实数，值域为1，1正弦函数的原函数或者说反函数就是csc函数或者说是余割函数，它是通过取sin函数的倒数来定义的所以，可以说csc的原函数是sin也就是说，如果我们对于任何一个函数。

上一篇： wps无法启动打印作业，wps无法启动打印作业是什么原因

下一篇： 我的帕瓦罗蒂观后感，我的帕瓦罗蒂电影原型